

Before we can calculate the density of carriers in a semiconductor, we have to find the number of available states at each energy. The number of electrons at each energy is then obtained by multiplying the number of states with the probability that a state is occupied by an electron. Since the number of energy levels is very large and dependent on the size of the semiconductor, we will calculate the number of states per unit energy and per unit volume. |
2.4.1 Calculation of the density of states |      |
The density of states in a semiconductor equals the density per unit volume and energy of the number of solutions to Schrödinger's equation. We will assume that the semiconductor can be modeled as an infinite quantum well in which electrons with effective mass, m*, are free to move. The energy in the well is set to zero. The semiconductor is assumed a cube with side L. This assumption does not affect the result since the density of states per unit volume should not depend on the actual size or shape of the semiconductor. |
The solutions to the wave equation (equation 1.2.14) where V(x) = 0 are sine and cosine functions: |
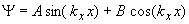 | (2.4.1) |
Where A and B are to be determined. The wavefunction must be zero at the infinite barriers of the well. At x = 0 the wavefunction must be zero so that only sine functions can be valid solutions or B must equal zero. At x = L, the wavefunction must also be zero yielding the following possible values for the wavenumber, kx. |
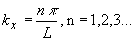 | (2.4.2) |
This analysis can now be repeated in the y and z direction. Each possible solution then corresponds to a cube in k-space with size nπ/L as indicated on Figure 2.4.1. |
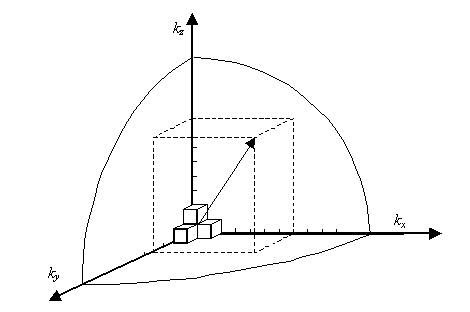 |
| Figure 2.4.1: | Calculation of the number of states with wavenumber less than k. |
The total number of solutions with a different value for kx, ky and kz and with a magnitude of the wavevector less than k is obtained by calculating the volume of one eighth of a sphere with radius k and dividing it by the volume corresponding to a single solution, |
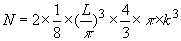 | (2.4.3) |
A factor of two is added to account for the two possible spins of each solution. The density per unit energy is then obtained using the chain rule: |
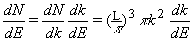 | (2.4.4) |
The kinetic energy E of a particle with mass m* is related to the wavenumber, k, by: |
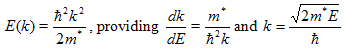 | (2.4.5) |
And the density of states per unit volume and per unit energy, g(E), becomes: |
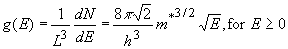 | (2.4.6) |
The density of states is zero at the bottom of the well as well as for negative energies. |
The same analysis also applies to electrons in a semiconductor. The effective mass takes into account the effect of the periodic potential on the electron. The minimum energy of the electron is the energy at the bottom of the conduction band, Ec, so that the density of states for electrons in the conduction band is given by: |
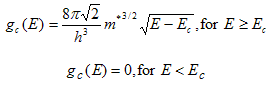 | (2.4.7) |
| Example 2.3 | Calculate the number of states per unit energy in a 100 by 100 by 10 nm piece of silicon (m* = 1.08 m0) 100 meV above the conduction band edge. Write the result in units of eV-1. |
| Solution | The density of states equals:
So that the total number of states per unit energy equals:
|
| Boulder, 2022 |