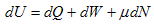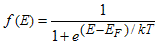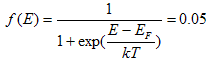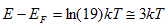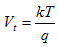Thermodynamics describes the behavior of systems containing a large number of particles. These systems are characterized by their temperature, volume, number and the type of particles. The state of the system is then further described by its total energy and a variety of other parameters including its entropy. Such a characterization of a system is much simpler than trying to keep track of each particle individually, hence its usefulness. In addition, such a characterization is general in nature, so that it can be applied to mechanical, electrical and chemical systems.

The term thermodynamics is somewhat misleading as one deals primarily with systems in thermal equilibrium. These systems have constant temperature, volume and number of particles and their macroscopic parameters do not change over time, so that the dynamics are limited to the microscopic dynamics of the particles within the system.

Statistical thermodynamics is based on the fundamental assumption that all possible configurations of a given system, which satisfy the given boundary conditions such as temperature, volume and number of particles, are equally likely to occur. The overall system will therefore be in the statistically most probable configuration, different ways to occupy the available energy levels, while satisfying the given boundary conditions. The entropy of such system is defined as the logarithm of the number of possible configurations multiplied with Boltzmann's constant. While such definition does not immediately provide insight into the meaning of entropy, it does provide a straightforward analysis since the number of configurations can be calculated for any given system.

Classical thermodynamics provides the same concepts. However, those were obtained through experimental observation. The classical analysis is therefore more tangible compared to the abstract mathematical treatment of the statistical approach.

The study of semiconductor devices requires some specific results, which naturally emerge from statistical thermodynamics. In this section, we review basic thermodynamic principles as well as some specific results. These include the thermal equilibrium concept, the thermodynamic identity, the basic laws of thermodynamics, the thermal energy per particle, the Fermi function and the thermal voltage .

1.4.1. Thermal equilibrium

A system is in thermal equilibrium if detailed balance is obtained; i.e. every microscopic process in the system is exactly balanced by its inverse process so that there is no net effect on the system.

This definition implies that in thermal equilibrium no net energy (heat, work or particle energy) is exchanged between the parts within the system or between the system and the environment. Thermal equilibrium is obtained by isolating a system from its environment, removing any internal sources of energy, and waiting for a long enough time until the system does not change any more.

The concept of thermal equilibrium is of interest since various thermodynamic results assume that the system under consideration is in thermal equilibrium. Few systems of interest rigorously satisfy this condition so that we often apply the thermodynamical results to systems that are "close" to thermal equilibrium. Agreement between theories based on this assumption and experiments justify this approach.

1.4.2. Laws of thermodynamics

Three laws must be postulated. These cannot be proven in any way and have been developed though the observation of a large number of systems.

The first law is common knowledge to most people and the classical form of the second law is clearly consistent with everyday observation. The third law can be further explained (but not proven) based on the definition provided above. As the temperature approaches zero Kelvin, the thermal energy approaches zero as well. As particles have less thermal energy, they will be more likely to occupy the lowest possible energy states of a given system. This reduces the number of possible configurations since fewer and fewer states can be occupied. As the temperature approaches zero Kelvin, the number of configurations and hence the entropy becomes constant.

1.4.3. The thermodynamic identity

The thermodynamic identity states that a change in energy can be caused by adding heat, work or particles. Mathematically this is expressed by:

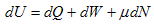(1.4.1)

where U is the total energy, Q is the heat and W is the work. μ is the energy added to a system when adding one particle without adding either heat or work. This energy is also called the electro-chemical potential. N is the number of particles.

1.4.4. The Fermi energy

The Fermi energy, EF, is the energy associated with a particle, which is in thermal equilibrium with the system of interest. The energy is strictly associated with the particle and does not consist even in part of heat or work. This same quantity is called the electro-chemical potential, μ, in most thermodynamics texts.

1.4.5. Some useful thermodynamics results

Listed below are two results, which will be used while analyzing semiconductor devices. The actual derivation is beyond the scope of this text.

The thermal energy of a particle, whose energy depends quadratically on its velocity, equals kT/2 per degree of freedom, where k is Boltzmann's constant. This thermal energy is a kinetic energy, which must be added to the potential energy of the particle. The thermal energy of a non-relativistic electron, which is allowed to move in three dimensions, equals 3/2 kT. Consider an electron occupying an energy level at energy, E,which is in thermal equilibrium with a large system characterized by a temperature T and Fermi energy EF. The probability that this electron occupies such energy level is given by:

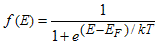(1.4.2)

The function f(E) is called the Fermi function and applies to all particles with half-integer spin. These particles, also called Fermions, obey the Pauli exclusion principle, (as intriduced in section 1.2.6, which states that no two Fermions in a given system can have the exact same set of quantum numbers. Since electrons are Fermions, their probability distribution also equals the Fermi function.

Example 1.5	Calculate the energy relative to the Fermi energy for which the Fermi function equals 5%. Write the answer in units of kT.
Solution	The problems states that: 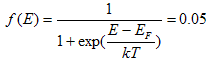which can be solved yielding: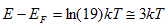

Finally, we need to introduce the thermal voltage, Vt, the potential an electron needs to traverse to gain an energy equal to the thermal energy kT. This voltage equals the thermal energy divided by the electronic charge, q, of the electron:

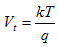(1.4.3)

The numeric value of the thermal voltage in Volt also equals the thermal energy in units of electron-Volt. At 300K (27oC) Vt equals 25.86 mV.