ρ, the charge density |
n, the electron density |
p, the hole density |
|
φ, the potential |
Ei, the intrinsic energy |
Fn, the electron quasi-Fermi energy |
Fp, the hole quasi-Fermi energy |
Jn, the electron current density |
Jp, the hole current density |
The drift-diffusion model of a semiconductor is frequently used to describe semiconductor devices. It contains all the features described in this chapter. |
Starting with Chapter 3, we will apply the drift-diffusion model to a variety of different devices. To facilitate this analysis, we present here a simplified drift-diffusion model, which contains all the essential features. This model results in a set of ten variables and ten equations. |
The assumptions of the simplified drift-diffusion model are: |
Full ionization: all dopants are assumed to be ionized (shallow dopants) |
Non-degenerate: the Fermi energy is assumed to be at least 3 kT below/above the conduction/valence band edge. |
Steady state: All variables are independent of time. |
Constant temperature: The temperature is constant throughout the device. |
The ten variables are the following: |
ρ, the charge density |
n, the electron density |
p, the hole density |
|
φ, the potential |
Ei, the intrinsic energy |
Fn, the electron quasi-Fermi energy |
Fp, the hole quasi-Fermi energy |
Jn, the electron current density |
Jp, the hole current density |
The ten equations are: |
Charge density equation |
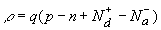 | (2.10.1) |
Electric field and potential equations |
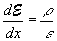 | (2.10.2) |
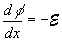 | (2.10.3) |
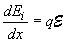 | (2.10.4) |
Carrier density equations |
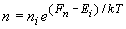 | (2.10.5) |
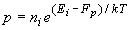 | (2.10.6) |
Drift and diffusion current equations |
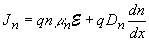 | (2.10.7) |
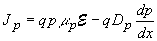 | (2.10.8) |
Continuity equation in steady state with SHR recombination |
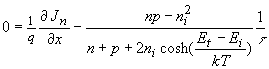 | (2.10.9) |
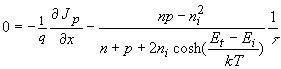 | (2.10.10) |
| Boulder, 2022 |