1.3 Electromagnetic Theory

1.3.1. Gauss's law
1.3.2. Poisson's equation

The analysis of most semiconductor devices includes the calculation of the electrostatic potential within the device as a function of the existing charge distribution. Electromagnetic theory and more specifically electrostatic theory are used to obtain the potential. A short description of the necessary tools, namely Gauss's law and Poisson's equation, is provided below.

1.3.1 Gauss's law

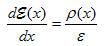Gauss's law is one of Maxwell's equations (Appendix 10) and provides the relation between the charge density, ρ, and the electric field, . In the absence of time dependent magnetic fields, the one-dimensional equation is given by:

(1.3.1)

This equation can be integrated to yield the electric field for a given one-dimensional charge distribution:

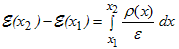(1.3.2)

Gauss's law as applied to a three-dimensional charge distribution relates the divergence of the electric field to the charge density:

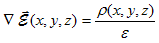(1.3.3)

This equation can be simplified if the field is constant and normal to each point of a closed surface, A, while enclosing a charge Q, yielding:

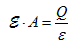(1.3.4)

Example 1.4

Consider an infinitely long cylinder with charge density, ρ, dielectric constant, ε₀ and radius, r₀. What is the electric field in and around the cylinder?

Solution

Because of the cylinder symmetry, one expects the electric field to be only dependent on the radius, r. Applying Gauss's law, equation (1.3.4), one finds:

and

where a cylinder with length L was chosen to define the surface A, and edge effects were ignored. The electric field then equals:

The electric field therefore increases within the cylinder with increasing radius as shown in the figure below. The electric field decreases outside the cylinder.

1.3.2 Poisson's equation

The electric field is defined as minus the gradient of the electrostatic potential, φ, or, in one dimension, as minus the derivative of the electrostatic potential:

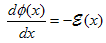(1.3.5)

The electric field vector therefore originates at a point of higher potential and points towards a point of lower potential.

The potential can be obtained by integrating the electric field as described by:

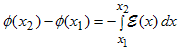(1.3.6)

At times, it is convenient to link the charge density to the potential by combining equation (1.3.5) with Gauss's law in the form of equation (1.3.1), yielding:

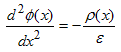(1.3.7)

which is referred to as Poisson's equation.

For a three-dimensional field distribution, the gradient of the potential is described by:

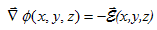(1.3.8)

and can be combined with Gauss's law as formulated with equation (1.3.3), yielding a more general form of Poisson's equation:

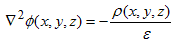(1.3.9)