
4.4.7. Heterojunction Diode Current



4.4.1. General discussion |      |
The current in a p-n diode is due to carrier recombination or generation somewhere within the p-n diode structure. Under forward bias, the diode current is due to recombination. This recombination can occur within the quasi-neutral regions, within the depletion region or at the metal-semiconductor Ohmic contacts. Under reverse bias, the current is due to generation. Carrier generation due to light will further increase the current under forward as well as reverse bias. |
In this section, we first derive the ideal diode current. We will also distinguish between the "long" diode and "short" diode case. The "long" diode expression applies to p-n diodes in which recombination/generation occurs in the quasi-neutral region only. This is the case if the quasi-neutral region is much larger than the carrier diffusion length. The "short" diode expression applies to p-n diodes in which recombination/generation occurs at the contacts only. In a short diode, the quasi-neutral region is much smaller than the diffusion length. In addition to the "long" and "short" diode expressions, we also present the general result for p-n diodes with arbitrary widths. |
Next, we derive expressions for the recombination/generation in the depletion region. Here we have to distinguish between the different recombination mechanisms - band-to-band recombination and Shockley-Hall-Read recombination - as they lead to different current-voltage characteristics. |
4.4.2. The ideal diode current |      |
When calculating the current in a p-n diode one needs to know the carrier density and the electric field throughout the p-n diode which can then be used to obtain the drift and diffusion current. Unfortunately, this requires the knowledge of the quasi-Fermi energies, which is only known if the currents are known. The straightforward approach is to simply solve the drift-diffusion equations listed in section 2.10 simultaneously. This approach however does not yield an analytic solution. |
To avoid this problem we will assume that the electron and hole quasi-Fermi energies in the depletion region equal those in the adjacent n-type and p-type quasi-neutral regions. We will derive an expression for "long" and "short" diodes as well as a general expression, which is to be used if the quasi-neutral region is comparable in size to the diffusion length. |
The primary assumption of the diode current derivation is that most recombination occurs in the quasi-neutral regions as defined based on the full depletion approximation (section 4.3.2). We also assume that the quasi-Fermi energies are constant throughout the depletion region as can be visualized on Figure 4.2.4b. This leads to the needed boundary values, namely the minority carrier densities at the edges of the depletion region. These values are obtained from equations (2.6.26) and (2.6.27) where we use the Fermi energy of the opposite region, yielding: |
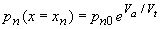 | (4.4.1) |
and |
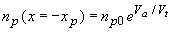 | (4.4.2) |
These equations can be verified to yield the thermal-equilibrium carrier density for zero applied voltage. In addition, an increase of the applied voltage will increase the separation between the two quasi-Fermi energies by the applied voltage multiplied with the electronic charge as also indicated on Figure 4.4.1. |
 |
| Figure 4.4.1 : | Position of the quasi-Fermi energies in a p-n diode. |
Next, we identify the minority carrier density at the contacts. Here we assume that the carrier density at the metal contacts equals the thermal-equilibrium carrier density. This assumption implies that excess carriers immediately recombine when reaching either of the two metal-semiconductor contacts. As recombination is typically higher at a semiconductor surface and is further enhanced by the presence of the metal, this is found to be a reasonable assumption. This results in the following set of boundary conditions: |
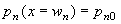 | (4.4.3) |
and |
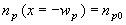 | (4.4.4) |
We are now ready to solve the diffusion equation and apply these boundary conditions. |
The general expression for the ideal diode current is obtained by applying the boundary conditions to the general solution of the diffusion equation for each of the quasi-neutral regions, as described by equation (2.9.13) and (2.9.14): |
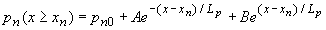 | (2.9.13) |
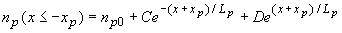 | (2.9.14) |
The boundary conditions at the edge of the depletion regions are described by (4.4.1), (4.4.2), (4.4.3) and (4.4.4). |
Before applying the boundary conditions, it is convenient to rewrite the general solution in terms of hyperbolic functions: |
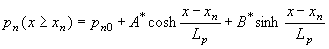 | (4.4.5) |
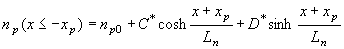 | (4.4.6) |
where A*, B*, C* and D* are constants whose value remains to be determined. Applying the boundary conditions then yields: |
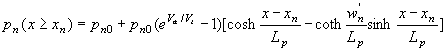 | (4.4.7) |
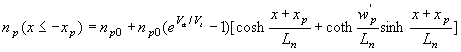 | (4.4.8) |
Where the quasi-neutral region widths, wn' and wp', are defined as: |
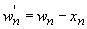 | (4.4.9) |
and |
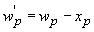 | (4.4.10) |
The current density in each region is obtained by calculating the diffusion current density using equations (2.7.24) and (2.7.25): |
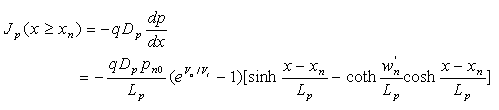 | (4.4.11) |
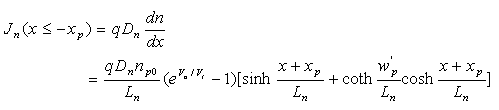 | (4.4.12) |
The total current must be constant throughout the structure since a steady state case is assumed. No charge can accumulate or disappear somewhere in the structure so that the charge flow must be constant throughout the diode. The total current then equals the sum of the maximum electron current in the p-type region, the maximum hole current in the n-type regions and the current due to recombination within the depletion region. The maximum currents in the quasi-neutral regions occur at either side of the depletion region and can therefore be calculated from equations (4.4.11) and (4.4.12). Since we do not know the current due to recombination in the depletion region we will simply assume that it can be ignored. Later, we will more closely examine this assumption. The total current is then given by: |
 | (4.4.13) |
Where the saturation current, Is, equals: |
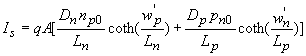 | (4.4.14) |
A diode with a "long" quasi-neutral region has a quasi-neutral region, which is much larger than the minority-carrier diffusion length in that region, or wn' > Lp and wp' > Ln. The general solution can be simplified under those conditions using: |
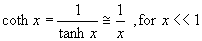 | (4.4.15) |
yielding the following carrier densities, current densities and saturation currents: |
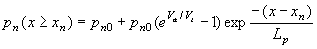 | (4.4.16) |
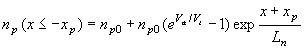 | (4.4.17) |
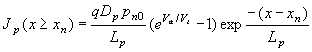 | (4.4.18) |
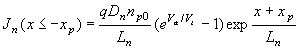 | (4.4.19) |
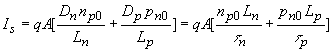 | (4.4.20) |
We now come back to our assumption that the current due to recombination in the depletion region can be simply ignored. Given that there is recombination in the quasi-neutral region, it would be unreasonable to suggest that the recombination rate would simply drop to zero in the depletion region. Instead, we assume that the recombination rate is constant in the depletion region. To further simplify the analysis we will consider a p+-n junction so that we only need to consider the recombination in the n-type region. The current due to recombination in the depletion region is then given by: |
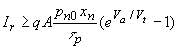 | (4.4.21) |
so that Ir can be ignored if: |
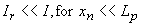 | (4.4.22) |
A necessary, but not sufficient requirement is therefore that the depletion region width is much smaller than the diffusion length for the ideal diode assumption to be valid. Silicon and germanium p-n diodes usually satisfy this requirement, while gallium arsenide p-n diodes rarely do because of the short carrier lifetime and diffusion length. |
As an example we now consider a silicon p-n diode with Na = 1.5 x 1014 cm-3 and Nd = 1014 cm-3. The minority carrier lifetime was chosen to be very short, namely 400 ps, so that most features of interest can easily be observed. We start by examining the electron and hole density throughout the p-n diode, shown in Figure 4.4.1: |
 |
| Figure 4.4.2 : | Electron and hole density throughout a forward biased p-n diode. |
The majority carrier densities in the quasi-neutral region simply equal the doping density. The minority carrier densities in the quasi-neutral regions are obtained from equations (4.4.16) and (4.4.17). The electron and hole densities in the depletion region are calculating using the assumption that the electron/hole quasi-Fermi energy in the depletion region equals the electron/hole quasi-Fermi energy in the quasi-neutral n-type/p-type region. The corresponding band diagram is shown in Figure 4.4.2: |
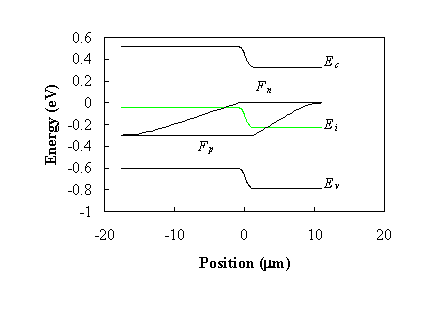 |
The quasi-Fermi energies were obtained by combining (4.4.16) and (4.4.17) with (2.10.5) and (2.10.6). Note that the quasi-Fermi energies vary linearly within the quasi-neutral regions. |
Next, we discuss the current density. Shown in Figure 4.4.3 is the electron and hole current density as calculated using (4.4.18) and (4.4.19). The current due to recombination in the depletion region was assumed to be constant. |
 |
| Figure 4.4.4 : | Electron and hole current density versus position. The vertical lines indicate the edges of the depletion region. |
A "short" diode is a diode with quasi-neutral regions, which are much shorter than the minority-carrier diffusion lengths. As the quasi-neutral region is much smaller than the diffusion length one finds that recombination in the quasi-neutral region is negligible so that the diffusion equations are reduced to: |
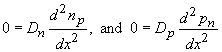 | (4.4.23) |
The resulting carrier density varies linearly throughout the quasi-neutral region and in general is given by: |
 | (4.4.24) |
where A, B, C and D are constants obtained by satisfying the boundary conditions. Applying the same boundary conditions at the edge of the depletion region as above (equations (4.4.3) and (4.4.4)) and requiring thermal equilibrium at the contacts yields: |
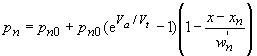 | (4.4.25) |
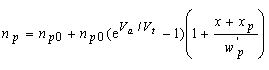 | (4.4.26) |
for the hole and electron density in the n-type and p-type quasi-neutral region. |
The current in a "short" diode is again obtained by adding the maximum diffusion currents in each of the quasi-neutral regions and ignoring the current due to recombination in the depletion region, yielding: |
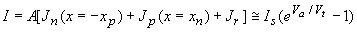 | (4.4.27) |
where the saturation current, Is is given by: |
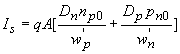 | (4.4.28) |
Alternatively one can obtain the "short" diode solution from the general solution, equation (4.4.14) using: |
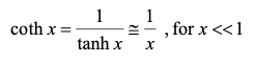 | (4.4.29) |
Since wn' << Lp and wp' << Ln. |
A comparison of the "short" diode expression with the "long" diode expression reveals that they are the same except for the use of either the diffusion length or the quasi-neutral region width in the denominator, whichever is smaller. |
Now that we have two approximate expressions, it is of interest to know when to use one or the other. To this end, we now consider a one-sided n+-p diode.The p-type semiconductor has a width, wp, and we normalize the excess electron density relative to its value at the edge of the depletion region (x = 0). The Ohmic contact to the p-type region is ideal so that the excess density is zero at x = wp'. The normalized excess carrier density is shown in Figure 4.4.4 for different values of the diffusion length. |
 |
| Figure 4.4.5: | Excess electron density versus position as obtained by solving the diffusion equation with dn(x = 0) = 1 and dn(x/wp' = 1) = 0 . The ratio of the diffusion length to the width of the quasi-neutral region is varied from 0.1 (Bottom curve), 0.3, 0.5, 1 and ´ (top curve) |
The figure illustrates how the excess electron density changes as the diffusion length is varied relative to the width of the quasi-neutral region. For the case where the diffusion length is much smaller than the width (Ln << wp'), the electron density decays exponentially and the "long" diode expression can be used. If the diffusion length is much longer than the width (Ln >> wp'), the electron density reduces linearly with position and the "short" diode expression can be used. If the diffusion length is comparable to the width of the quasi-neutral region width one must use the general expression. A numeric analysis reveals that the error is less than 10 % when using the short diode expression with Ln > 2 wp' and when using the long diode expression with Ln < wp'/2. Note that the best approximation is not necessarily the same in each region of the same p-n diode. |
| Example 4.4 | An abrupt silicon p-n junction (Na = 1016 cm-3 and Nd = 4 x 1016 cm-3) is biased with Va = 0.6 V. Calculate the ideal diode current assuming that the n-type region is much smaller than the diffusion length with wn' = 1 mm and assuming a "long" p-type region. Use mn = 1000 cm2/V-s and mp = 300 cm2/V-s. The minority carrier lifetime is 10 ms and the diode area is 100 mm by 100 mm. |
| Solution | The current is calculated from:
with
yielding I = 40.7 mA Note that the hole diffusion current occurs in the "short" n-type region and therefore depends on the quasi-neutral width in that region. The electron diffusion current occurs in the "long" p-type region and therefore depends on the electron diffusion length in that region. |
4.4.3. Recombination-Generation current |      |
We now calculate the recombination-generation current in the depletion region of a p-n junction. We distinguish between two different possible recombination mechanisms: band-to-band recombination and Shockley-Hall-Read recombination. |
The recombination/generation current due to band-to-band recombination/generation is obtained by integrating the net recombination rate, Ub-b, over the depletion region: |
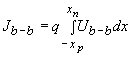 | (4.4.30) |
where the net recombination rate is given by (2.8.3): |
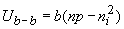 | (4.4.31) |
The carrier densities can be related to the constant quasi-Fermi energies and the product is independent of position: |
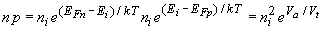 | (4.4.32) |
This allows the integral to be solved analytically yielding: |
 | (4.4.33) |
The current due to band-to-band recombination has therefore the same voltage dependence as the ideal diode current and simply adds an additional term to the expression for the saturation current. |
The current due to trap-assisted recombination in the depletion region is also obtained by integrating the trap-assisted recombination rate over the depletion region width: |
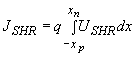 | (4.4.34) |
Substituting the expression (2.8.4) for the recombination rate yields: |
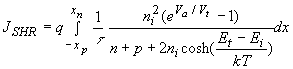 | (4.4.35) |
where the product of the electron and hole densities was obtained by assuming that the quasi-Fermi energies are constant throughout the depletion region, which leads to: |
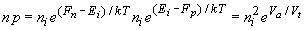 | (4.4.36) |
The maximum recombination rate is obtained when the electron and hole densities are equal and therefore equals the square root of the product yielding: |
 | (4.4.37) |
From which an effective width can be defined which, when multiplied with the maximum recombination rate, equals the integral of the recombination rate over the depletion region. This effective width, x', is then defined by: |
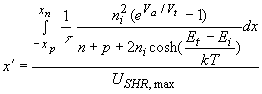 | (4.4.38) |
and the associated current due to trap-assisted recombination in the depletion region is given by: |
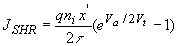 | (4.4.39) |
This does not provide an actual solution since the effective width, x', still must be determined by performing a numeric integration. Nevertheless, the above expression provides a way to obtain an upper estimate by substituting the depletion layer width, xd, as it is always larger than the effective width. |
A numeric solution to equation (4.4.38) for a symmetric abrupt silicon (ni=1010cm-3) p-n junction is presented in Figure 4.4.6. |
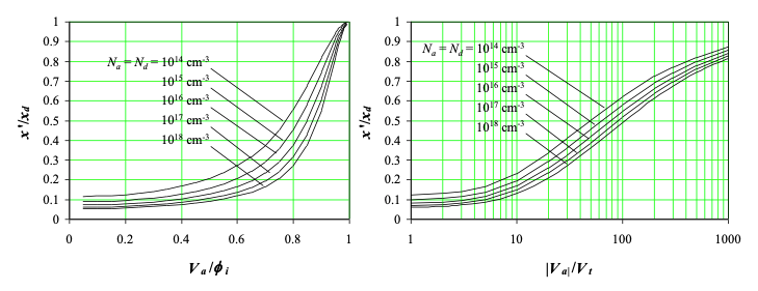 |
| Figure 4.4.6: | Normalized effective width, x'/xd, under a) forward bias and b) reverse bias, of a symmetric abrupt silicon p-n junction |
As can be seen on the figure, the effective width ranges from 0.1 xd to xd, depending on the bias voltage and doping density. Higher forward/reverse bias results in a more uniform recombination rate in the depletion region, hence a larger effective width. |
Combining both types of recombination in the depletion layer (4.4.32) and (4.4.39) with the general current equation (4.4.14), we obtain an expression that is universally applicable: |
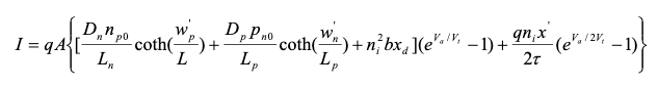 | (4.4.40) |
4.4.4. I-V characteristics of real p-n diodes |      |
The forward biased I-V characteristics of real p-n diodes are further affected by high injection and the series resistance of the diode. To illustrate these effects while summarizing the current mechanisms discussed previously we consider the I-V characteristics of a silicon p+-n diode with Nd = 4 x 1014 cm-3, tp = 10 μs, and μp = 450 cm2/V-s. The I-V characteristics are plotted on a semi-logarithmic scale and four different regions can be distinguished as indicated on Figure 4.4.5. First, there is the ideal diode region where the current increases by one order of magnitude as the voltage is increased by 60 mV. This region is referred to as having an ideality factor, n, of one. This ideality factor is obtained by fitting a section of the curve to the following expression for the current: |
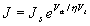 | (4.4.41) |
The ideality factor can also be obtained from the slope of the curve on a semi-logarithmic scale using: |
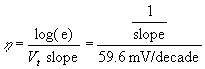 | (4.4.42) |
where the slope is in units of V/decade. To the left of the ideal diode region there is the region where the current is dominated by the trap-assisted recombination in the depletion region described in section 4.4.3.2. This part of the curve has an ideality factor of two. To the right of the ideal diode region, the current becomes limited by high injection effects and by the series resistance. |
High injection occurs in a forward biased p-n diode when the injected minority carrier density exceeds the doping density. High injection will therefore occur first in the lowest doped region of the diode since that region has the highest minority carrier density. |
Using equations (4.4.1) and (4.4.2), one finds that high injection occurs in a p+-n diode for the following applied voltage: |
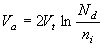 | (4.4.43) |
or at Va = 0.55 V for the diode of Figure 4.4.5 as can be verified on the figure as the voltage where the ideality factor changes from one to two. For higher forward bias voltages, the current no longer increases exponentially with voltage. Instead, it increases linearly due to the series resistance of the diode. This series resistance can be due to the contact resistance between the metal and the semiconductor, due to the resistivity of the semiconductor or due to the series resistance of the connecting wires. This series resistance increases the external voltage, Va*, relative to the internal voltage, Va, considered so far. |
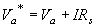 | (4.4.44) |
Where I is the diode current and Rs is the series resistance. |
These four regions can be observed in most p-n diodes although the high-injection region rarely occurs, as the series resistance tends to limit the current first. |
 |
| Figure 4.4.7: | Current-Voltage characteristics of a silicon diode under forward bias. |
4.4.5. The diffusion capacitance |      |
As a p-n diode is forward biased, the minority carrier distribution in the quasi-neutral region increases dramatically. In addition, to preserve quasi-neutrality, the majority carrier density increases by the same amount. This effect leads to an additional capacitance called the diffusion capacitance. |
The diffusion capacitance is calculated from the change in charge with voltage: |
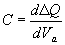 | (4.4.45) |
Where the charge, DQ, is due to the excess carriers. Unlike a parallel plate capacitor, the positive and negative charge is not spatially separated. Instead, the electrons and holes are separated by the energy bandgap. Nevertheless, these voltage dependent charges yield a capacitance just as the one associated with a parallel plate capacitor. The excess minority-carrier charge is obtained by integrating the charge density over the quasi-neutral region: |
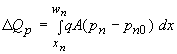 | (4.4.46) |
We now distinguish between the two limiting cases as discussed when calculating the ideal diode current, namely the "long" diode and a "short" diode. The carrier distribution, pn(x), in a "long" diode is illustrated by Figure 4.4.6 (a). |
 |
| Figure 4.4.8: | Minority carrier distribution in (a) a "long" diode, and (b) a "short" diode. The excess minority-carrier charge, ΔQp, in the quasi-neutral region, is proportional to the area defined by the solid and dotted lines. |
Using equation (4.4.18), the excess charge, ΔQp, becomes: |
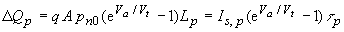 | (4.4.47) |
where Is,p is the saturation current for holes, given by: |
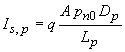 | (4.4.48) |
Using Lp2 = Dp τp. Equation (4.4.45) directly links the excess charge to the diffusion current. Since all injected minority carriers recombine in the quasi-neutral region, the current equals the excess charge divided by the average time needed to recombine with the majority carriers, i.e. the carrier lifetime, τp. |
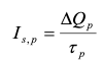 | (4.4.49) |
This relation will be the corner stone of the charge control model of bipolar junction transistors (section 5.6.2). |
The diffusion capacitance then equals: |
 | (4.4.50) |
Similarly, for a "short" diode, as illustrated by Figure 4.4.6 (b), one obtains: |
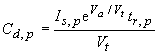 | (4.4.51) |
Where tr,p is the hole transit time given by: |
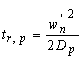 | (4.4.52) |
Again, the excess charge can be related to the current. However, in the case of a "short" diode all minority carriers flow through the quasi-neutral region and do not recombine with the majority carriers. The current therefore equals the excess charge divided by the average time needed to traverse the quasi-neutral region, i.e. the transit time, tr,p. |
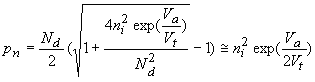 | (4.4.53) |
The total diffusion capacitance is obtained by adding the diffusion capacitance of the n-type quasi-neutral region to that of the p-type quasi-neutral region. |
The total capacitance of the junction equals the sum of the junction capacitance, discussed in section 4.3.4, and the diffusion capacitance. For reverse biased voltages and small forward bias voltages, one finds that the junction capacitance is dominant. As the forward bias voltage is further increased the diffusion capacitance increases exponentially and eventually becomes larger than the junction capacitance. |
| Example 4.5 |
|
| Solution |
|